Dados 3 puntos de una circunferencia, ¿es posible encontrar siempre un cuarto punto de manera que sean vértice de:
a) un rectángulo?
b) un trapecio?
c) un rombo?
d) Enuncien las condiciones que deben cumplir dichos puntos en cada caso.
En esta actividad, a diferencia de las anteriores, no se dan las condiciones de construcción del cuadrilátero, sino que el alumno debe pensarlas teniendo en cuenta las propiedades de cada uno de ellos.
En principio es necesario comenzar a estudiar dónde puedan encontrarse esos puntos de la circunferencia.
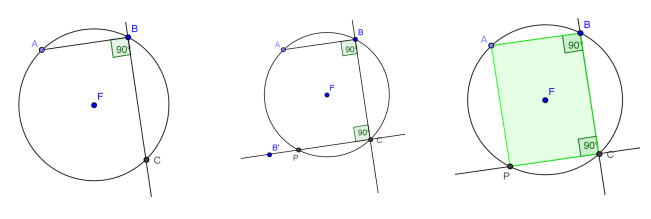
Para el ítem a), los estudiantes podrían pensar que, como el cuadrilátero debe ser un rectángulo, entonces debe tener ángulos rectos. Entonces, ¿cómo ubicar estos tres vértices para que determinen un ángulo recto? Será necesario aquí recuperar la idea de que si el ángulo inscripto es recto, entonces abarca una cuerda correspondiente a un diámetro.
Ahora bien, el ítem b) agrega una variante, ya que los tres puntos elegidos sobre la circunferencia, A, B y C, pueden ser cualquier terna de puntos, pero para que determinen un trapecio es necesario que tenga al menos un par de lados paralelos. Esta cuestión habilita a encontrar dos posibles puntos P que cumplan con esa condición. Podría ser que AB//CP o que BC//AP. También puede suceder que los alumnos no advirtieran estas dos posibilidades y entendieran que el problema queda resuelto encontrando una única posibilidad. En ese caso, sería necesario un espacio de la clase para compartir los distintos trapecios hallados. Si ningún estudiante hubiera advertido que es posible obtener dos trapecios diferentes según qué lados son los que se eligen como paralelos, sería interesante que el docente instale la pregunta sobre esta cuestión, habilitando el espacio compartido de la clase para seguir estudiando estas figuras y buscando razones para estar seguros de que son solo esas y no existen otras más.
Otro detalle interesante a analizar es la ubicación que no puede tener el tercer punto:
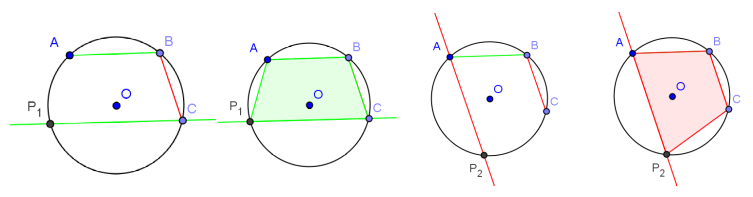
No podría estar en la mediatriz del segmento que se está eligiendo como base del trapecio. Si así lo fuera el tercer y cuarto punto coincidirían formando un triángulo isósceles y no un trapecio. El último ítem de esta actividad instala otra cuestión bien diferente. ¿Cómo encontrar un rombo inscripto en una circunferencia? ¿Es esto posible? Podría ser que los alumnos comiencen por explorar las posibilidades para tres puntos cualquiera A, B y C y en los intento por lograr la equidistancia para que determinen lados congruentes, adviertan que AC debe ser diámetro, en cuyo caso, recuperando las ideas anteriores, el ABC debería ser recto. ¿Existen rombos con ángulos rectos? ¿Qué sucede si un rombo tiene un ángulo recto? ¿Cómo resultan los restantes? Todas estas cuestiones, que pueden surgir de los intentos por encontrar un rombo inscripto, son interesantes de analizar con toda la clase. Esta situación permite además recuperar la clasificación inclusiva de los cuadriláteros. Un docente advertido de estas cuestiones sabrá retomar las ideas vertidas en el diálogo con los alumnos para que encuentren razones para estar seguros de que el único rombo posible de inscribir en una circunferencia es el cuadrado.