Las actividades de la secuencia
Se anticipa en este apartado el enunciado de cada una de las actividades que conforman esta secuencia a fin de poder tener una primera aproximación del recorrido completo que se propone.
Al finalizar este apartado se ofrecen notas y comentarios que incluyen posibles modos de resolución de los alumnos y posibles intervenciones docentes con la intención de, por un lado comprender la organización de la secuencia y, por el otro, pensar la gestión de la clase de manera que todos los estudiantes puedan hacer matemática siendo parte de “una comunidad de producción.”
Al combinar figuras en una construcción es posible relacionarlas y apoyarse en sus propiedades para argumentar acerca de la validez de esas relaciones. Por ejemplo, al trazar algunos ángulos en una circunferencia y modificar la medida de uno, se modifica la medida de otro: ¿Por qué ocurre esto?
La exploración de figuras inscriptas en una circunferencia permitirá identificar sus propiedades para encontrar algunas explicaciones.
Actividad 0: Explorar e identificar relaciones
Parte 1
En una circunferencia, de radio igual a 4 cm y centro O, marquen un punto P. Dibujen un ángulo con vértice en P, de manera que uno de los lados del ángulo corte a la circunferencia en un punto A y el otro coincida con un diámetro PB. Ahora construye un ángulo cuyo vértice sea O y sus lados pasen por los puntos A y B.
a) Existe una relación entre la amplitud del ángulo APB, al que llamaremos inscripto y el AOB, al que llamaremos central, que no contiene a P. Encuentren y enuncien esta relación.
Parte 2
En otra circunferencia de centro Q, marcar R y dibujando un ángulo con vértice en R, de manera que uno de los lados del ángulo corte a la circunferencia en un punto C y el otro la corte en el punto D.
b) La relación enunciada en el ítem a) ¿sigue siendo válida o no? ¿Por qué?
c) ¿Se mantiene la relación enunciada en el ítem a), si cambia el valor del radio de la circunferencia? ¿Cómo pueden explicarlo?
d) ¿Seguirá siendo válida la relación enunciada en el ítem a) si el punto P no pertenece a la circunferencia?
Actividad 1: Averiguar medidas sin medir
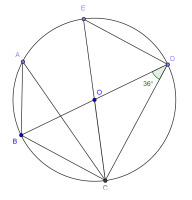
A, B, C, D, E son puntos de la circunferencia de centro O y los puntos BDC forman un ángulo de 36° y BD es diámetro. Como muestra la figura.
a) Sin medir, determinen la amplitud de cada uno de los siguientes ángulos COB, DEC, CAB y DCB.
b) Si varía el valor del ángulo BDC, ¿se modifica la amplitud de algún otro ángulo? ¿Por qué?
c) Para que exploren con Geogebra: ¿será cierto que la suma de los ángulos DEC y BDC es siempre un recto? Justifiquen.
Actividad 2: Explorar para encontrar explicaciones
Utilizando Geogebra tracen un segmento AC. Marquen su punto medio O y tracen la circunferencia de centro O que pase por A. Marquen un punto B en la circunferencia y tracen la recta BO, luego marquen el punto D en la intersección entre la recta y la circunferencia. Construyan el cuadrilátero ABCD. ¿Es cierto que siempre el cuadrilátero obtenido es un rectángulo? Justifiquen su respuesta.
Actividad 3: Construir y establecer relaciones
a) Construyan un triángulo APB donde el ángulo APB sea recto.
b) Tracen la mediana PO, correspondiente al lado AB del triángulo
c) ¿Qué relación existe entre los ángulos OAP y OPA? ¿Y entre OPB y OBP?
d) Marquen el punto C tal que APBC sea un rectángulo. Justifiquen
e) ¿Es cierto que los vértices del rectángulo APBC pertenecen a una misma circunferencia? Justifiquen.
Actividad 4: Producir construcciones para encontrar condiciones
Dados 3 puntos de una circunferencia, ¿es posible encontrar siempre un cuarto punto de manera que sean vértice de:
a) un rectángulo?
b) un trapecio?
c) un rombo?
d) Enuncien las condiciones que deben cumplir dichos puntos en cada caso.
Actividad 5: Interpretar y decidir
Existe una propiedad que dice que: Un cuadrilátero es inscriptible si la suma de un par de ángulos opuestos es 180°.
Analiza lo que afirmaron dos alumnos al intentar la demostración y decide si estás de acuerdo con alguno de ellos, explica por qué estás de acuerdo o por qué no.
Patricia: “Si la suma de un par de ángulos opuestos es 180°, entonces la suma del otro par de ángulos también tiene que ser 180°porque la suma de los ángulos interiores de un cuadrilátero es 360°.”
Clara: “Yo consideré, sin medir, que los arcos de los ángulos opuestos de cualquier cuadrilátero inscripto, abarcan toda la circunferencia”
Actividad 6: Recuperar relaciones estudiadas
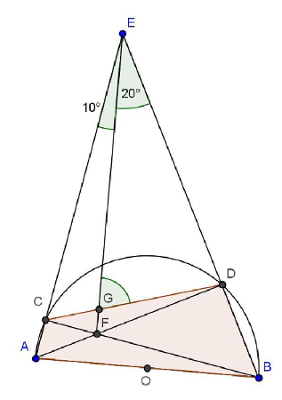
Encuentren la amplitud del ángulo EGD sin medirlo, sabiendo que ABDC es un cuadrilátero inscripto en una semicircunferencia y que el ángulo CEG= 10°, y el ángulo GED=20°.
EC y ED son las prolongaciones de AC y BD respectivamente.
Actividad 7: ¿Es verdad?
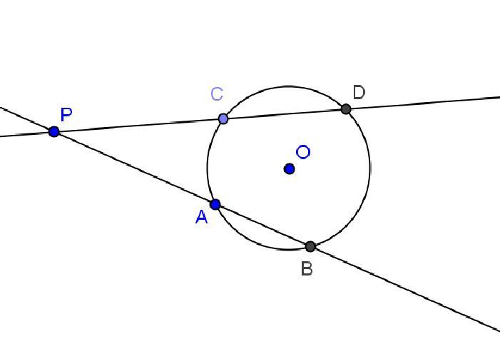
a) ¿Será cierto que los triángulos APD y PBC que quedan determinados por dos rectas que cortan a una circunferencia en A, B y C, D respectivamente y se intersectan en un punto P, son semejantes?
b) ¿Y qué PA . PB = PC . PD?
Actividad 8: ¿Por qué es verdad?
Claudio Ptolomeo nació en Egipto aproximadamente en el año 85 d.C. y murió en Alejandría en el año 165 d.C. Astrónomo y Geógrafo, propuso el sistema geocéntrico como la base de la mecánica celeste que perduró por más de 1400 años. Su trabajo consistió en estudiar la gran cantidad de datos existentes sobre el movimiento de los planetas con el fin de construir un modelo geométrico que explicase dichas posiciones en el pasado y fuese capaz de predecir sus posiciones futuras.
Un aporte interesante que hizo al conocimiento matemático de su época fue el que hoy conocemos como teorema de Ptolomeo, que dice lo siguiente:
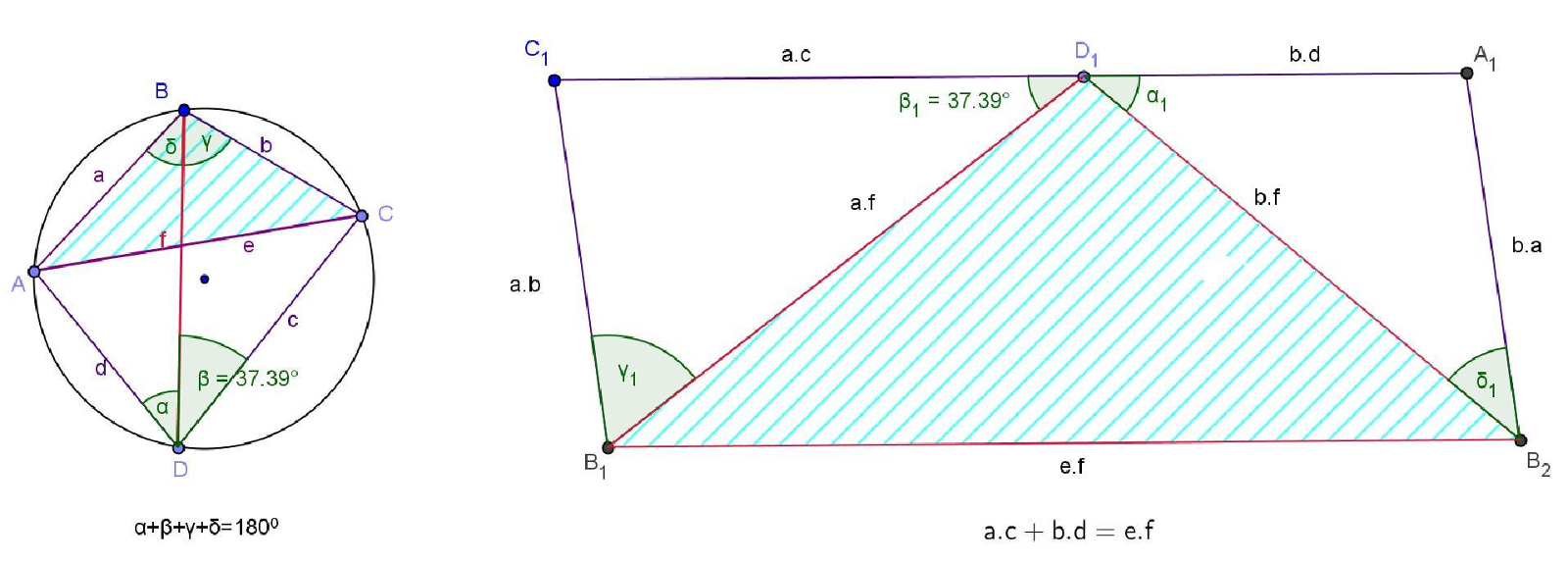
En todo cuadrilátero inscripto, la suma de los productos de lados opuestos es igual al producto de sus diagonales.
- ¿Qué construcciones podrían realizar con Geogebra que les permitan explorar esta relación enunciada por Ptolomeo?
- Analicen las siguientes construcciones e intenten averiguar por qué es verdadero lo que afirma Ptlomeo.
Actividad 9: Decidir y argumentar
Analicen la veracidad de estas afirmaciones. En caso de falsedad den un contraejemplo y modifiquen la oración para hacerla verdadera. En caso de ser verdadera justifiquen.
a) Todos los paralelogramos son inscriptibles.
b) Ningún trapecio es posible de inscribir en una circunferencia.
c) Todo romboide es inscriptible, si su diagonal principal es diámetro.
d) El ángulo que forma una diagonal de un cuadrilátero inscripto con un lado de ese cuadrilátero, es congruente con el que forma la otra diagonal con el lado opuesto al anterior.
e) En todo cuadrilátero inscripto ABCD, se cumple que AO.OC=BO.OD, si O es el punto de intersección de sus diagonales.