Para dialogar entre colegas
Propuesta 1
En parejas o grupos pequeños, resolver la Actividad 0.
¿Qué posibilidades brinda el uso de Geogebra en situaciones de exploración?
“Lo que caracteriza los dibujos dinámicos es la capacidad de ser modificados por un movimiento continuo de sus componentes, asegurando que la propiedades geométricas de dicho objeto se mantienen invariantes. Esto quiere decir que toda propiedad geométrica se traduce en un fenómeno visual que se produce al arrastrar los objetos, de manera que el arrastre se convierte en un medio de reconocimiento y de verificación de las propiedades geométricas en un dibujo dinámico” (Acosta Gempeler, 2004, p.5).
Propuesta 2
Entendemos que los problemas admiten en su mayoría distintos modos de resolución. ¿Por qué nos interesa promover en el aula esta variedad de estrategias?
Se propone analizar el modo en que los alumnos resuelven la Actividad 1 de esta secuencia pensando en:
- ¿Qué conocimientos ponen en juego cada uno de estos alumnos?
- ¿Cómo organizarían el intercambio entre los alumnos en el momento de la puesta en común?
Antonio: 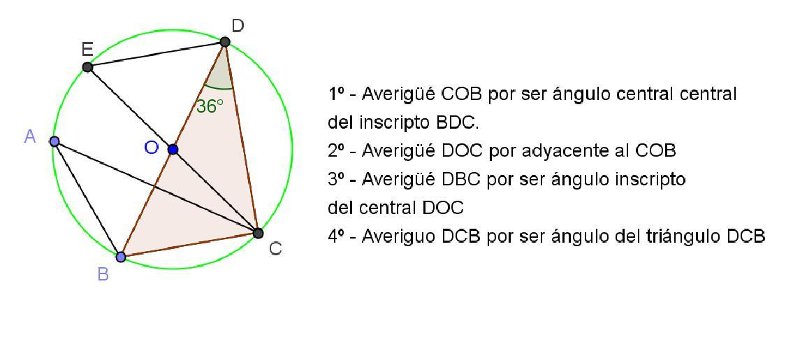
Belén:
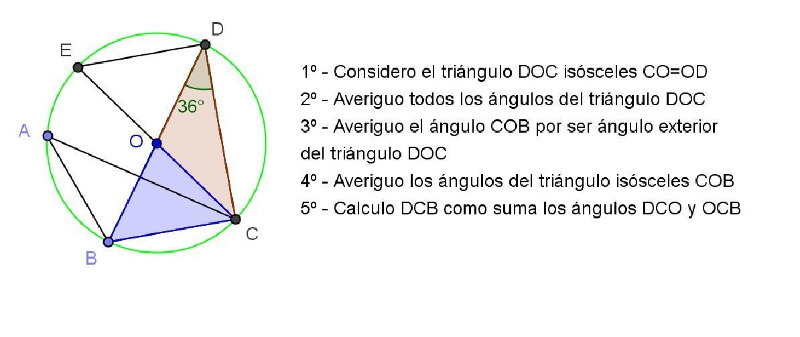
Carla:
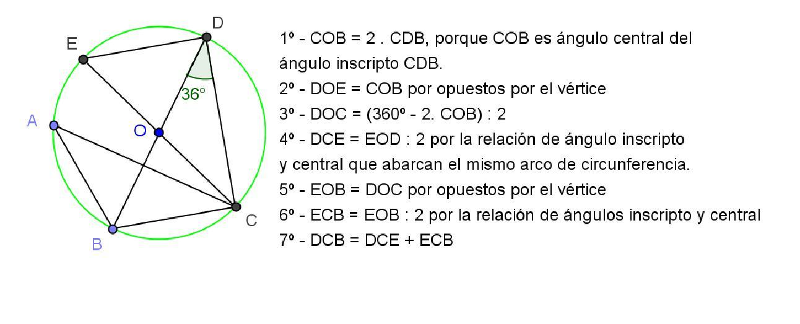
“Las exigencias de explicitación, de argumentación, de revisión y de validación, brindan oportunidades para transformar el conocimiento y hacerlo más reconocible; por esto, son elementos esenciales de la constitución del sentido de los conocimientos. Estas prácticas permitirán que los alumnos aprendan “otra cosa” respecto del mismo objeto matemático y se apropien al mismo tiempo de los modos de producción característicos de la matemática” (Saiz y Parra, 2011: 8).
Propuesta 3
Resolver las Actividades 2, 3, 4 y 5 de la secuencia pensando en que en cada una se proponen distintos tipos de tareas: explorar, construir, justificar ¿Qué se privilegia en cada una de ellas?
Propuesta 4
¿Cuál es el rol del docente en una clase de geometría en la que se propone el uso de TIC?
La tecnología en sí misma no es garantía de aprendizaje si no hay un docente que tiene un claro propósito de enseñanza y actúa en consecuencia.
El interés de la propuesta consiste en involucrar a los alumnos en el desafío intelectual de encontrar pruebas para argumentar y aproximarse así al modo particular de validar en geometría.