Desarrollo de la secuencia: decisiones didácticas, anticipaciones y comentarios
Puntos de partida: ¿por qué una actividad 0?
Esta secuencia puede comenzar con la Actividad 0, una situación de exploración entre ángulos que comparten un mismo arco de circunferencia.
Es una actividad que tiene una doble finalidad. Por un lado, la familiarización del estudiante con el uso de Geogebra al realizar la construcción pedida y al realizar las exploraciones de los items c) y d). Se verá que el uso de este soft facilita la exploración pedida. La intención es que al aplicar el test de arrastre y mover los puntos puedan enunciar algunas conclusiones sobre los ángulos trazados en la circunferencia. En caso de que los alumnos no hayan trabajado con Geogebra aún, podría ser la oportunidad para presentarlo y explorar sus herramientas básicas.
Actividad 0: Explorar e identificar relaciones
Parte 1
En una circunferencia, de radio igual a 4 cm y centro O, marquen un punto P. Dibujen un ángulo con vértice en P, de manera que uno de los lados del ángulo corte a la circunferencia en un punto A y el otro coincida con un diámetro PB. Ahora construye un ángulo cuyo vértice sea O y sus lados pasen por los puntos A y B.
a) Existe una relación entre la amplitud del ángulo APB, al que llamaremos inscripto y el AOB, al que llamaremos central, que no contiene a P. Encuentren y enuncien esta relación.
Parte 2
En otra circunferencia de centro Q, marcar R y dibujando un ángulo con vértice en R, de manera que uno de los lados del ángulo corte a la circunferencia en un punto C y el otro la corte en el punto D.
b) La relación enunciada en el ítem a), ¿sigue siendo válida o no? ¿Por qué?
c) ¿Se mantiene la relación enunciada en el ítem a), si cambia el valor del radio de la circunferencia? ¿Cómo pueden explicarlo?
d) ¿Seguirá siendo válida la relación enunciada en el ítem a) si el punto P no pertenece a la circunferencia?
Por otra parte, esta actividad tiene la finalidad de poner a los alumnos frente a un primer problema que les permite recuperar algunas relaciones entre ángulos que ya fueron estudiadas. En el ítem a) se presenta un caso particular de ángulo inscripto, cuando uno de sus lados es diámetro de la circunferencia. Una alternativa de resolución es la de atender a que AOP es un triángulo isósceles con dos lados que son radios de la circunferencia y por eso APO y PAO son ángulos iguales. Luego, conociendo que la suma de ángulos interiores de un triángulo es igual a un llano y que BOP es llano, es posible concluir que APO (el inscripto) es igual a la mitad de AOB (el central). Otra alternativa es pensar que AOB es ángulo exterior del triángulo APO y por eso igual a la suma de los interiores no adyacentes.
En el ítem b) puede resultar que los alumnos elijan que el punto D en la misma semicircunferencia que C respecto del diámetro que pasa por RQ o no. En ambos casos, descomponiendo el inscripto y el central en dos partes, se obtiene la misma relación que en el caso particular sea por resta o por suma de los correspondientes ángulos. La relación por la que se pregunta en estos dos puntos a) y b) es la que se da entre ángulos inscriptos y sus ángulos centrales correspondientes.
Las conclusiones a las que se arribe en el debate podrán ser:
Todo ángulo inscripto en una circunferencia es igual a la mitad del ángulo central correspondiente.
Para resolver esta actividad los alumnos deberán realizar una construcción siguiendo indicaciones dadas para poder establecer la relación entre el ángulo inscripto y central. El uso de Geogebra facilita la etapa exploratoria, en la que se podrá elegir la herramienta crear una circunferencia dados su centro y su radio 
Esta herramienta permite indicar un punto que será el centro y determinar la medida del radio. Una vez creada la circunferencia se puede utilizar la herramienta renombrar para llamar O al centro de la circunferencia; por defecto el programa coloca el nombre “A”.
Luego será necesario elegir la herramienta  para crear un punto sobre la circunferencia, renombrarlo como “P” y crear los puntos A y B de la misma manera.
para crear un punto sobre la circunferencia, renombrarlo como “P” y crear los puntos A y B de la misma manera.
Se sugiere en este momento analizar con los alumnos la herramienta más conveniente para construir los lados del ángulo APB; si es la de crear un segmento o una semirrecta 
Si se elige crear semirrecta para hacer los lados del ángulo APB y el AOB podría cambiarse el color de los mismos para mayor impacto visual.
A continuación se puede imprimir el dibujo y trabajar sobre él, proponiendo a los alumnos “analizar los ángulos y triángulos señalados para establecer relaciones entre ellos”.
Los alumnos tendrán oportunidad de explicitar las relaciones que conocen además de la relación entre los ángulos inscripto y central. El docente podrá solicitar que se inicie o continúe un Registro de propiedades conocidas que funcionarán como punto de partida para encontrar otras nuevas y que irán conformando el conjunto de conocimientos compartidos de la clase.
Luego de realizar este registro, a modo de comprobación, se puede proponer
explorar el software para encontrar el modo de medir la amplitud de esos ángulos. El programa cuenta con la herramienta ángulo  que ofrece esta posibilidad, como se muestra en la siguiente figura:
que ofrece esta posibilidad, como se muestra en la siguiente figura:
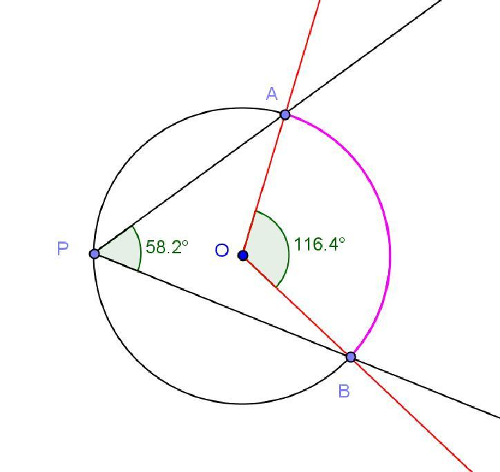
La intención de proponer la construcción de una circunferencia de radio libre parte c) de esta actividad es la de permitir a los estudiantes analizar que la relación entre en los ángulos inscriptos y centrales que abarcan el mismo arco de circunferencia, es independiente del radio de la misma. Los alumnos podrán visualizar que cambia el tamaño de la circunferencia pero la relación permanece constante.
Si el ítem c) de la actividad se hiciera sin emplear Geogebra y se realizaran las construcciones con lápiz y papel, los alumnos, posiblemente, realizarán una construcción diferente cada vez que quiera modificar el radio de la circunferencia y medir cada uno de los ángulos para analizar si la relación se mantiene o se modifica. Claro que esas mediciones, nos darán valores diferentes con lo que no se puede asegurar la existencia de la relación. Esta cuestión será una ocasión interesante para discutir sobre la certeza de las conclusiones que se obtienen razonando sobre propiedades conocidas a diferencia de las que se obtienen realizando mediciones efectivas, como se hizo al elaborar las conclusiones del Registro de propiedades. En el Geogebra, las mediciones no son efectivas sino que los valores resultan del uso de propiedades.
Una expresión posible de las conclusiones para este punto c) podría ser:
Esta relación no se modifica al cambiar el valor del radio porque siempre se forman triángulos isósceles cuyos ángulos de la base son iguales.
Para responder a la parte d) se debe crear otro punto no perteneciente a la circunferencia y determinar los ángulos APB y AOB cuyos lados abarcan el mismo arco de circunferencia, como se muestra en el siguiente dibujo:
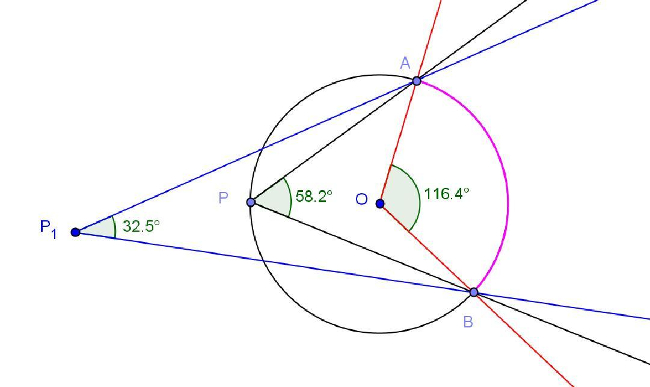
Se ofrece a los docentes, que se inician en el uso de Geogebra, interactuar con la propuesta en el applet para familiarizarse con este software y con los pasos que la hicieron posible.
Para estudiar los pasos de una construcción realizada con Geogebra es posible desplegar del menú VISTA la herramienta “Protocolo de construcción”; en una tabla interactiva se exponen los pasos de la construcción que permiten rehacer el dibujo realizado.
Notemos que se consideró un punto P1 exterior a la circunferencia y que también puede considerarse un punto interior.
Si el docente considera que no es necesaria esta actividad exploratoria ya sea para familiarizarse con Geogebra o para establecer las relaciones entre ángulos centrales y ángulos inscriptos en una circunferencia porque sus alumnos la conocen, podría comenzar la secuencia directamente con la Actividad 1.
En la mencionada Actividad 1 se propone la exploración de figuras y se avanza en un trabajo del tipo argumentativo que requiere el procedimiento de encadenar relaciones ya conocidas para deducir otras propiedades y relaciones. Esta situación se enmarca en la necesidad de introducirse en un pensar geométrico que privilegie la elaboración de conjeturas buscando abrir un camino hacia una validación mediante “pruebas intelectuales” (Balacheff, 1987), es decir, poniendo en juego propiedades de los objetos geométricos.
En las Actividades 2 y 3 los alumnos deberán realizar construcciones interpretando las indicaciones dadas en cada caso. Después de una etapa exploratoria con Geogebra, que implica mover los puntos libres de la circunferencia para obtener una variedad de casos para estudiar, se pasará a la búsqueda de razones por las cuales es posible afirmar que el cuadrilátero obtenido es un rectángulo. Si bien desde lo perceptivo es posible visualizar que, si la construcción está bien realizada, la forma del cuadrilátero no varía al mover los objetos libres, lo que el software no dice es por qué siempre que se mueven estos objetos la figura obtenida sigue siendo un rectángulo. Esta búsqueda de razones será parte del trabajo argumentativo requerido. Es necesario generar en las clases las condiciones para que el discurso forme parte de lo que es necesario considerar, de manera que el estudiante asuma la responsabilidad de aprender dando razones válidas sobre las afirmaciones que enuncia.
La Actividad 4 invita a explorar libremente distintas ubicaciones para los tres puntos de la circunferencia, y en estos intentos encontrar las condiciones para que con el cuarto punto determinen algunos cuadriláteros particulares. Posiblemente, en estos ensayos los alumnos encuentren que los puntos no pueden ser cualquiera y que también existen determinadas condiciones para que sea posible encontrar el cuarto vértice de manera que el cuadrilátero sea rectángulo, trapecio o rombo.
La Actividad 5 propone analizar el razonamiento empleado por otros estudiantes al intentar demostrar una propiedad de los cuadriláteros inscriptibles. Esta actividad requiere un esfuerzo particular de análisis al tener que decidir sobre la consistencia de los razonamientos expuestos.
La Actividad 6 retoma lo trabajado en las actividades anteriores y permite resignificar las propiedades de los ángulos inscriptos en una circunferencia, las congruencias de ángulos que abarcan el mismo arco y la condición que requiere un cuadrilátero para ser inscripto.
Las Actividades 7 y 8 apuntan a que los alumnos elaboren pruebas intelectuales, es decir que puedan justificar la verdad de la afirmación tomando distancia de la acción. La demostración de la semejanza de los triángulos requerirá de estas pruebas intelectuales.
La Actividad 9 pretende hacer una mirada para recapitular lo aprendido hasta el momento de manera que pueda ser reutilizado. La tarea de argumentar sobre la verdad o falsedad de las afirmaciones invita a los alumnos a volver sobre las actividades realizadas favoreciendo el reconocimiento de las propiedades involucradas, es decir, promueve un trabajo sobre los objetos geométricos que se ponen en juego.
En este recorrido de actividades se adoptó la decisión de partir de una fase exploratoria con la posibilidad de utilizar recursos tecnológicos, aunque no exclusivamente, para reconocer propiedades de las figuras y validarlas mediante pruebas intelectuales. Se recuerda que para que los estudiantes avancen hacia la elaboración de este tipo de pruebas es necesario que el docente acompañe generando condiciones desafiantes que avancen en la necesidad de usar las propiedades para justificar.