Actividad 1: Averiguar medidas sin medir
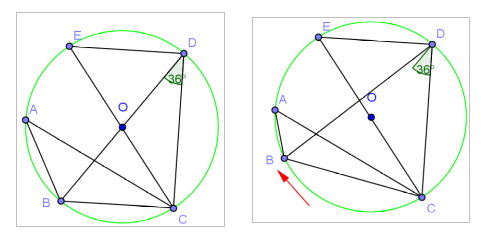
A, B, C, D, E son puntos de la circunferencia de centro O y los puntos BDC forman un ángulo de 36° y BD es diámetro. Como muestra la figura.
a) Sin medir, determinen la amplitud de cada uno de los siguientes ángulos COB, DEC, CAB y DCB.
b) Si varía el valor del ángulo BDC, ¿se modifica la amplitud de algún otro ángulo? ¿Por qué?
c) Para que exploren con Geogebra: ¿Será cierto que la suma de los ángulos DEC y BDC es siempre un recto? Justifiquen.
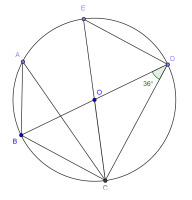
Para resolver la parte a) se espera que los alumnos puedan apoyarse en algunas relaciones y propiedades entre ángulos para averiguar las amplitudes solicitadas, por ejemplo, la referida a la suma de los ángulos interiores de un triángulo, o que identifiquen ángulos adyacentes, o que establezcan relaciones entre ángulos centrales e inscriptos. Es posible que en esta parte de la actividad surjan diferentes formas de averiguar la medida de los ángulos pedidos. Será interesante que se dedique un espacio de la clase a la socialización de estas distintas maneras de resolución, de este intercambio y de la explicitación de los procedimientos empleados surgirá la posibilidad de establecer otras relaciones que algunos alumnos tal vez no hubieran advertido en el momento de la resolución individual.
Estas podrían ser algunas de las explicaciones dadas por los estudiantes y posible de analizar con toda la clase. En cada una de ellas los conocimientos puestos en juego son bien diferentes, la elección de uno u otro dependerá de los conocimientos de los que dispongan de modo más afianzado.
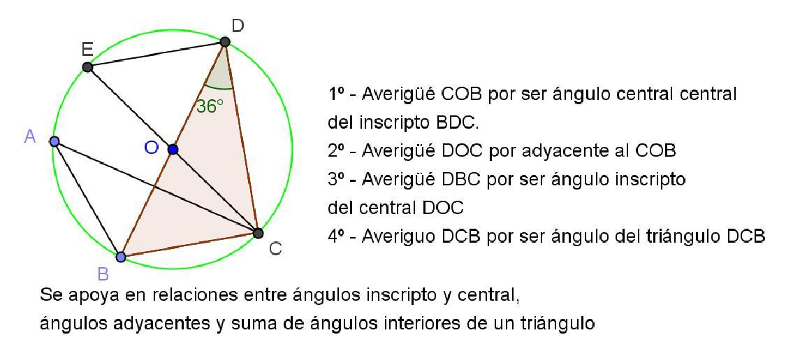
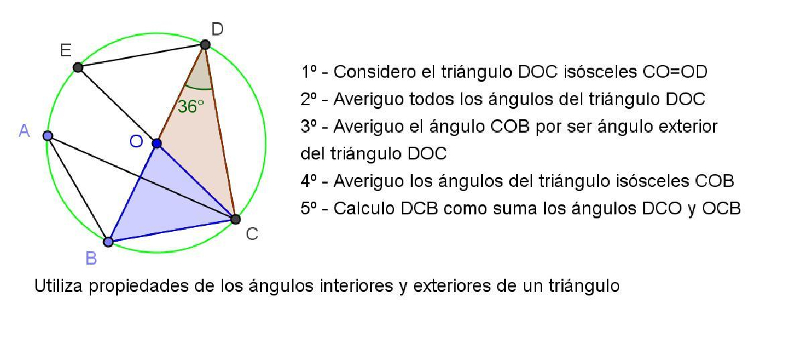
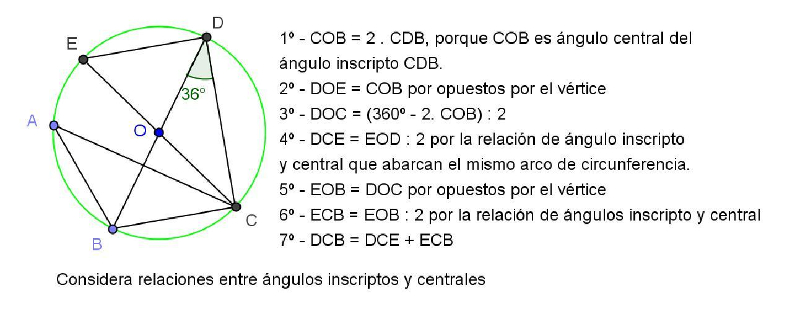
En este último procedimiento, el alumno se apoya en la percepción visual para la afirmación que realiza en el 2° paso, ya que al mover el punto E, EC deja de ser diámetro y por lo tanto los ángulos DOE y COB dejan de ser opuestos por el vértice. Esto podrá observarse al resolver el inciso c) cuando en la exploración con Geogebra descubran que EC no es siempre diámetro.
Si fuera de interés del docente hacer evidente algunas propiedades no utilizadas por los alumnos, como por ejemplo las relaciones entre ángulos centrales e inscriptos, y no hubieran surgido, podría proponerse a toda la clase analizar estas explicaciones dadas por otros estudiantes. En este caso el tipo de tarea cambia, ya que la parte a) de esta actividad solamente requiere averiguar la medida de determinados ángulos y analizar procedimientos de otros exige un nivel de razonamiento más complejo.
Para resolver esta actividad se requiere del copiado de la figura con modelo presente, cada alumno deberá tenerla visible, podrá ser entregada en una fotocopia o ser expuesta con un proyector de imágenes o en el pizarrón, otra opción podría ser pegar la imagen en la vista gráfica del Geogebra.
Con Geogebra debe cuidarse la diferencia entre dibujar y construir. Para poder advertir esta diferencia el docente podrá proponer a sus alumnos usar la herramienta elige y mueve 
un punto, por ejemplo el B, y las condiciones iniciales no deberían cambiar, como se muestra más abajo donde al mover B el segmento BD deja de ser diámetro. Esta es una condición inicial que no debería modificarse al elegir un punto y moverlo.
La pregunta que se plantea en c) invita a explorar las relaciones entre dos ángulos, en particular el DEC y BDC. Podría ser que en principio los alumnos tomen a esta relación como un caso particular y dependiente del valor del ángulo dado, es decir que el valor de la suma dependa de la medida dada del ángulo BDC. Al haber realizado la construcción con Geogebra es posible rápidamente ver que esta relación no depende de la medida del ángulo dado. Ahora bien, la cuestión consiste en encontrar razones por las cuáles esta suma permanece invariante al cambiar la medida del ángulo BDC. Esta cuestión es la que se plantea en la parte b) en el que se invita a explorar qué ángulos son los que se modifican al variar la amplitud de BDC. Para averiguar esto será necesario considerar otros elementos de la figura construida, como son los arcos que abarcan estos ángulos DEC y BDC. Al advertir que entre estos dos ángulos se abarca un semicírculo, es posible relacionar este arco con el ángulo central que abarca el mismo arco, el BOD, ángulo llano. Conociendo la relación entre ángulo central y ángulo inscripto se podría enunciar la siguiente conclusión: