Reflexiones sobre la enseñanza de la geometría y el trabajo en el aula
Se considera la matemática como una construcción social, colectiva y a los resultados de la comunidad de matemáticos de una época, “sus productos”, como productos culturales condicionados por las concepciones de la sociedad en la que emergen. Pensar la actividad matemática de este modo y como una actividad de modelización permite integrar distintas facetas del trabajo matemático: la resolución de problemas, el uso de técnicas, la transformación de representaciones, la producción de pruebas.
Interesa particularmente que los estudiantes puedan involucrarse en la actividad de producción matemática, tomando como referencia el modo en que las ideas matemáticas han surgido en el seno de las comunidades de matemáticos. Recuperar algunos problemas clásicos de la historia de la matemática es una de las estrategias que permite este posicionamiento, por esta razón se incluye, entre otras cosas, el Teorema de Ptolomeo surgido en los intentos por interpretar geométricamente y modelizar el universo en el que pensaban que vivían en el siglo II de nuestra era.
El conjunto de actividades de esta secuencia pretende involucrar a los alumnos en el desafío de resolver problemas que les permitan movilizar “viejos” conocimientos y que, en los intentos por buscar la solución, puedan construir una respuesta estableciendo relaciones nuevas. Al respecto, Brousseau (1986) afirma: “El alumno aprende adaptándose a un medio que es factor de contradicciones, de dificultades, de desequilibrios, un poco como lo hace la sociedad humana. Este saber, fruto de la adaptación del alumno, se manifiesta por respuestas nuevas que son la prueba del aprendizaje”.
A pesar de que en los últimos años ha habido intentos por recuperar un espacio para la enseñanza de la geometría, aún sigue ausente en muchas aulas de nuestras escuelas secundarias. En nuestro país, algunos especialistas han profundizado en su estudio didáctico facilitándonos genuinos fundamentos para incluirla, como así también renovados modos de pensar su enseñanza.
“… si algo “se cae” del programa por falta de tiempo es la geometría. Al punto que nadie dudaría en promover a un alumno de quinto año de EGB a sexto por no conocer la propiedad de la suma de los ángulos interiores de un triángulo.
… se remarca este fenómeno con el fin de advertir que si esta tendencia continúa, se priva a los alumnos de la posibilidad de conocer otro modo de pensar, se les quita la posibilidad de vivir una experiencia de involucrarse con otras formas de razonamiento, que son específicas de este dominio.” H. Itzcovich (2005)
El estudio de las propiedades de las figuras y los cuerpos geométricos entraña mucho más que reconocerlas perceptivamente y saber sus nombres. Implica conocer, cada vez con mayor profundidad sus propiedades y poder tenerlas disponibles para resolver diversos tipos de problemas. El “modo de pensar geométrico” supone poder apoyarse en propiedades y relaciones estudiadas de las figuras y de los cuerpos para poder anticipar otras no conocidas. Por otra parte, permite saber que dicho resultado es el correcto porque las propiedades puestas en juego lo garantizan.
Si bien en los primeros años de la escolaridad, lo perceptivo y la experiencia cobran un lugar preponderante para poder analizar figuras y enunciar propiedades, es de esperar que en la escuela secundaria el modo de demostrar la validez de una afirmación no sea empírico, por ejemplo midiendo o dibujando, sino que se base en razonamientos deductivos. Es decir, la experiencia geométrica de los alumnos a lo largo de la escolaridad pueda recorrer un camino que comience con un tipo de trabajo empírico, para avanzar hacia un trabajo de tipo argumentativo, en el que se entienda que los cuerpos y las figuras no pertenecen a un espacio físico sino a un espacio matematizado, y por ende las validaciones no sean constatadas “observando” o “midiendo”, sino apoyándose en las propiedades conocidas de esos objetos geométricos.
Ahora bien, ¿qué situaciones proponer a los alumnos para que sean un “factor de contradicciones, de dificultades, de desequilibrios” y movilicen los conocimientos disponibles para producir otros nuevos? Carmen Sessa describe algunas características que debiera reunir una situación para considerarse un problema. En “Acerca de la enseñanza de la geometría” afirma que para que una situación sea un problema geométrico para los alumnos, es necesario que:
- “Implique un cierto nivel de dificultad, presente un desafío, tenga algo de “novedad” para los alumnos.
- Exija usar los conocimientos previos, pero que estos no sean totalmente suficientes.
- Para resolverlos, se deban poner en juego las propiedades de los objetos geométricos.
- El problema ponga en interacción al alumno con objetos que ya no pertenecen al espacio físico, sino a un espacio conceptualizado representado por las figuras cuerpos.
- En la resolución de problemas, los dibujos no permitan arribar a la respuesta por simple constatación sensorial.
- La validación de la respuesta dada al problema –es decir, la decisión del alumno acerca de la verdad o falsedad de la respuesta– no se establezca empíricamente, sino que se apoye en las propiedades de los objetos geométricos; aunque en algunas instancias exploratorias, se puedan aceptar otros modos de corroborar.
- Las argumentaciones a partir de las propiedades conocidas de los cuerpos y figuras produzcan un nuevo conocimiento acerca de estos últimos.” (Sessa, C., 1998)
Por ejemplo, las construcciones son fuente de interesantes problemas geométricos, ya que son actividades en las que es posible que las propiedades conocidas y la exploración de otras, surjan como respuesta al problema. En ellas es necesario considerar que la utilización de algunos instrumentos favorece o moviliza el uso de algunas propiedades más que otras y que esto puede ser una decisión del docente según sus intenciones de enseñanza.
Véase, en el siguiente ejemplo, cómo la restricción de los instrumentos geométricos a emplear pone en juego propiedades diferentes de las rectas paralelas:
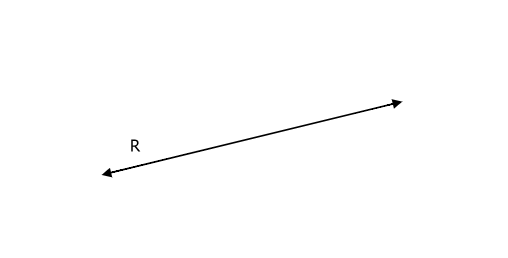
a) Con regla y escuadra traza una recta paralela a la recta dada:
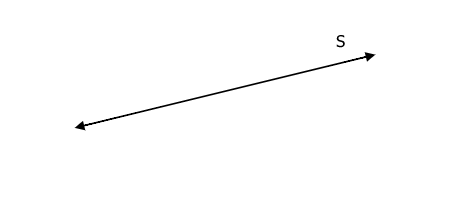
b) Con compás y regla no graduada traza una recta paralela a la siguiente:
c) Con Geogebra dos rectas paralelas, sin usar la herramienta Rectas Paralelas 
de manera que al una de ellas, se mueva la otra y sigan siendo paralelas.
En cada uno de estos ítems, la construcción solicitada es la misma: “trazar rectas paralelas”, pero los conocimientos que se movilizan para lograr este objetivo, con la restricción del recurso solicitado, podrían ser diferentes. El instrumento geométrico empleado (regla, compás, escuadra) sería, en este caso, una variable posible de administrar por el docente en función de los conocimientos que desea que los alumnos pongan en juego en cada caso.
En el caso a) al utilizar regla y escuadra para trazar rectas paralelas, la propiedad puesta en juego es: Si dos rectas son perpendiculares a una tercera, son paralelas entre sí. Tal vez el alumno no sepa cómo expresar esta propiedad, sino que su conocimiento se basa en la experiencia de colocar la regla y la escuadra en determinada posición para poder trazar rectas paralelas. Es fundamental que estas ideas se hagan explícitas, se recomienda que el docente gestione un espacio de la clase que favorezca la reflexión para que este conocimiento pueda ser enunciado.
En el caso b) los conocimientos que se movilizan son otros. Aquí para trazar una recta paralela, es necesario apelar, aunque sea intuitivamente, a la noción de distancia y pensar que: Una recta paralela a una dada es el lugar geométrico de todos los puntos que están a igual distancia de esta última. De esa manera es posible con el compás encontrar al menos dos puntos que estén a igual distancia de sendos puntos de la recta para trazar la recta que pasa por ellos y que resultará paralela a la dada.
En el caso c) se pide el uso de la tecnología, en particular en este caso el uso de Geogebra.
Esto genera en muchos alumnos un interés particular, que los lleva a investigar cómo funciona, cuáles son las posibilidades que brinda esa herramienta y de qué manera facilita la tarea solicitada. Una cuestión interesante a tener en cuenta es que este software permite que el docente pueda restringir el uso de determinadas herramientas. Por ejemplo, si se quisiera que los alumnos exploren las herramientas, se podría dejar disponible el ícono Rectas paralelas.
Para esta alternativa, se podría en primer lugar trazar una recta, determinar un punto exterior a la misma y seleccionar la herramienta Rectas paralelas “tocando” la recta y el punto creado.
Si en cambio interesara movilizar los conocimientos involucrados en esa construcción, como la noción de equidistancia o las propiedades de rectas perpendiculares y paralelas, sería necesario restringir el uso de la herramienta Rectas paralelas cuestión que Geogebra permite realizar con facilidad ocultándola provisoriamente.
Geogebra es un software libre de geometría dinámica, basado en una filosofía altruista: los programas se elaboran para compartirlos. Disponible en la web